2. 플로이드 와샬

 

플로이드 와샬을 사용하는 경우는?

플로이드 와샬은 그래프 알고리즘 중 하나라고 할 수 있다.

각각의 정점에서 다른 각각의 정점으로 가는 최단거리를 구하는 알고리즘이다.

이게 무슨 소리일까?

처음에는 다른 블로그들을 봤을 때 잘 이해가 안갔었는데, 이해하고 나서 막상 쓰려다보니 저 말이 맞는 말이다.

이해가 잘 안갔던 기억을 토대로 이 글에서 좀 자세하게 알고리즘에 대해 설명 해보고자 한다.

 

 

플로이드 와샬 알고리즘

아래 그림을 살펴본다.

단순히 그래프를 직관적으로 봤을 때, 출발지에서 도착지까지 어딘가 경유하지 않고 한 번에 갈 수 있는 거리를 오른쪽 표로 나타낸 것이다.

이제부터 오른쪽 표를 하나씩 채워가며 완성할 건데, 이때 모든 칸들을 최솟값으로 채우는 알고리즘이 바로 플로이드 와샬 알고리즘이다.

즉,

1번에서 1번으로 가는 모든 경우의 수 중에 최소,

1번에서 2번으로 가는 모든 경우의 수 중에 최소,

...

4번에서 4번으로 가는 모든 경우의 수 중 최소.

여기서 모든 경우의 수라는 것은, 출발지에서 도착지까지 한번에 가는 거리와 어찌저찌 경유해서 가는 모든 거리의 수를 말한다.

 

알고리즘은 아래와 같다.

• 위 그림에서 오른쪽 표의 초기값은 출발지에서 도착지로 한번에 가는 경우이다.
• 나머지 빈칸들은 무한(e.g. Integer.MAX_VALUE)으로 설정해놓는다.
• 초기값이 한번에 가는 경우의 수이기 때문에, 이제부터는 경유해서 도착하는 경우만 생각하면 된다.
  • 1번을 경유할 때,
    1 -> 1 -> 1로 가는 거리 , 1 -> 1 -> 2로 가는 거리, 1 -> 1 -> 3으로 가는 거리, 1 -> 1 -> 4로 가는 거리
    2 -> 1 -> 1로 가는 거리, 2 -> 1 -> 2로 가는 거리, 2 -> 1 -> 3으로 가는 거리, 2 -> 1 -> 4로 가는 거리
    ....
    4 -> 1 -> 1로 가는 거리, ... , 4 -> 1 -> 4로 가는 거리
    
    
  • 2번을 경유할 때,
    1 -> 2 -> 1로 가는 거리, 1 -> 2 -> 2로 가는 거리, 1 -> 2 -> 3으로 가는 거리, ..
    ....
    
    
  • 각 노드를 경유할 때마다, 표에다가 거리 값을 적어보면 어떤 값들이 변경되는 지 알 수 있다.
• 위와 같이 경유할 노드(k)를 하나 정해놓고, 출발(i) 에서 도착(j)로 가는 값과 이미  출발(i)에서 도착(j)까지 가는 거리가 저장되어 있는 값과 비교하여 더 작은 값을 채워나가면 된다.
• 즉,  맨 위의 표를 board[][] 라는 배열이라고 할 때,
  board[i][k]+board[k][j] 와 board[i][j]를 비교해서 더 작은 값을 board[i][j]에 갱신해가는 것이다.

 

참고로 위 그래프를 완성시키면 아래와 같이 완성될 것이다.

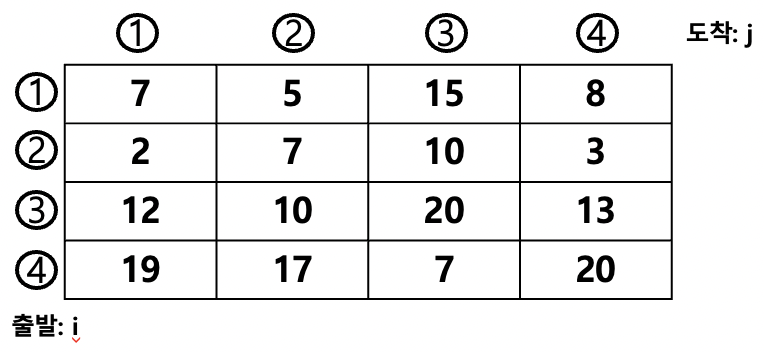
소스코드

플로이드 와샬 알고리즘을 구현하면 아래와 같이 구현될 것이다.

for(int k=0; k<n; k++) { // 경유지
    for(int i=0; i<n; i++) { // 출발지
        for(int j=0; j<n; j++) { // 도착지
			
            board[i][j] = Math.min(board[i][j], board[i][k]+board[k][j]);
            
        }
    }
}